
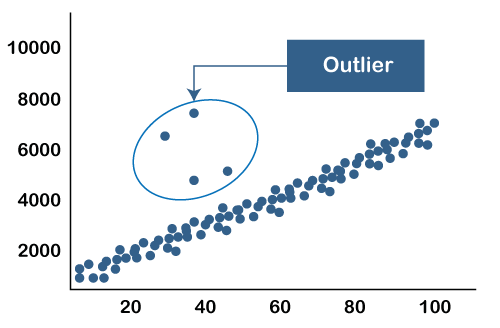
In other cases, outliers might be mistakes in the data that may adversely affect statistical analysis of the data. In some cases, outliers can be beneficial to understanding special characteristics of the data.

Often they are extreme values that fall outside the “normal” range of the data. Outliers are data points that do not match the general character of the data. The python implementation is pretty straightforward, most of the outlier detection algorithms are available in this neat package called pyod.About Blog Project Outlier Identification Using Mahalanobis Distance ABOF of A.Īs the main criterion is the variance of angles and distance only acts as the weight, ABOD is able to detect outliers even in high dimensional data where other purely distance-based approaches fail. If we compute the variance of this value over all pairs of points from the query point A then we get angle-based outlier factor i.e. This weighting factor is important because the angle to a pair of points varies naturally stronger for bigger distances. With this weighting factor in the denominator, the distance does influence the ABOF value, but only to a minor extent. the angle is weighted less if the corresponding points are far from the query point. In the formula we can see that we not only calculate the angle between the vectors in the numerator but also that they are normalized by the quadratic product of the length of the difference vectors in the denominator, i.e. ABOF(A) is the variance of the angles between the point A to all other points in the dataset D The angle-based outlier factor of a point A i.e. Let’s assume 3 points (A, B, C ) in the database D. How is it measured quantitatively?ĪBOD uses ABOF(Angle Based Outlier Factor) to determine the outlierness of a point. This means that the point is positioned outside of some sets of points that are grouped together. When the spectrum of angles from a point to all other points is small that means other points are positioned in certain directions only. When the spectrum of angles from a point to all other points is broad that means it is surrounded by points in all possible directions, so it is inside a cluster of points Hence, the spectrum of angles to pairs of points remains rather small for an outlier whereas the variance of angles is higher for border points of a cluster and very high for inner points in a cluster of points. Hence here the variance of the angles is much smaller.
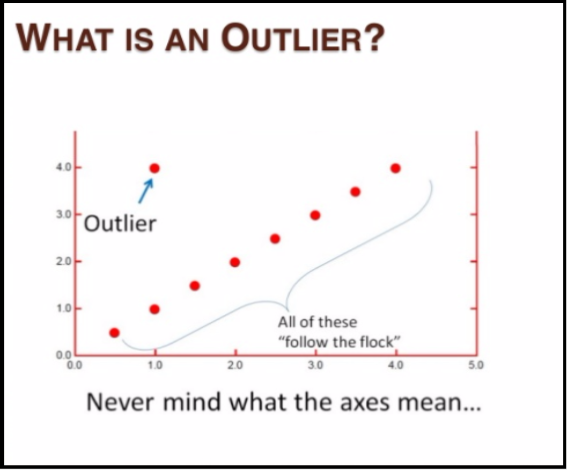
We can clearly notice that the angles are much narrower as all of them pointing in the same direction. This can be mathematically described by the below formula where the relative difference between the farthest point and the nearest point converges to 0 for increasing dimensionality d: The haziness is due to the well know bottleneck in machine learning called “The curse of dimensionality”, as the number of dimensions increases the concept of distance makes lesser sense as all data points are so far off in the euclidean space that the relative difference in the distance doesn’t matter much. Most of the outlier techniques rely on distance computations, If the data points distance is large from rest of the data points then it is deemed to be an outlier, for high-dimensional data the concept of distance becomes hazy. To overcome this we do something like Mahalanobis or MCD which would hold good a lot of times.īut now, in the big data era where companies are storing huge chunks of multi-dimensional data, the traditional multivariate outlier techniques start to show their drawbacks. In multi-dimensional data, if we perform a uni-dimensional outlier analysis using a box-plot on each individual dimension, we might not have a concrete answer because the same data point might be a potential outlier in a particular dimension and not an outlier in another dimension. Things get a little complicated when we go multi-dimensional. When dealing with Outliers, it is relatively straightforward to find outliers in a uni-dimensional setting where we could do a box plot and find potential outliers. We know what outliers are – the data points that lie outside of where most of our data lie.


 0 kommentar(er)
0 kommentar(er)
